Hidrodinamik Nedir?

Fiziğin hareket halindeki sıvılarla ilgilenen bölümü. Akışkanların hareketinin incelenmesi yalnızca birkaç özel hal için, basit sonuçların elde edilmesini sağlar; oldukça karmaşık olan matematiksel inceleme, ender olarak, gerçekten hesaplanabilir çözümlere erişilmesini sağlamaktadır.Getirilen basitleştirmeler, akışkanı ya da akışları ilgilendirir: Sürtünmeler göz önüne alınmadığında akışkana kusursuz, göz önüne alındığındaysa gerçek denir ve bu durumda ağdalılığın hesaba katılması gerekir. Akışlar, borular ve kanallar içinde incelenir­ler: bunlar çoğunlukla süreklidir, ancak, geçici de olabilirler. Birinci durumda taneciklerin yörüngesi uzamda sabit eğrilerden oluşur; hız­lar da zamandan bağımsızdır.

Deliklerden Akış

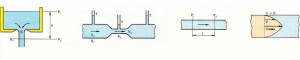
Sıvı kusursuz olarak kabul edildi­ğinde, buna Bernoulli teoremi uygulanabilir.Bu kuram -E-+ -VÎ+ z = sabit P9 2g bağıntısıyla açıklanabilir. Bu ba­ğıntıda p, söz konusu noktadaki basınç; p, özgül kütle; V, hız; g, yerçe­kimi ivmesi; Z ise noktanın bir refe­rans düzlemine göre konumudur. Bu bağıntı, ince bir duvara açılan bir delikten akış hızının saptanmasını sağlar (Çiz. 1). Deney, delik çıkışında, püsküren sıvının daraldığını ve silindir biçi­mini aldığını gösterir. Bir h yüksekli­ğinden akan sıvının hızı, aynı yük­seklikten serbest düşüş yaptığında kazanacağı hıza eşit olur. Bu açıklama Torricelli teoremini dile getir­mektedir. V hızıyla, sıvı damarının s₂ kesitinin çarpımı olan Q hacimsel debisi, deliğin s kesitinden hareketle de hesaplanabilir: Q = V.s₂ = a.s.V; bu­rada a, damarın daralma katsayısıdır ve basit bir delik için, 0,60 olan değeri, sıvı damarın biçimini alan bir tüp için l’e kadar değişebilir. Kap dış­bükeyse daralma daha az, dolayı­sıyla, debi de daha yüksektir. Fıski­yenin silindir görüntüsünün, kılcal­lık etkisiyle, hızla damla oluşumuna yol açan kabarıklıklar ve incelmeler dizisine dönüştüğünü burada belirt­mek gerekir.

Borularda Akış

Değişken kesitli yatay bir boru içinde, hız ve basınç kesite bağlı ola­rak değişir (Çiz. 2). Sı ve S₂ kesitle­rinde debi aynıysa Qı = Sı • Vı = Q₂ = S₂ • V₂ olur; böylece = ݲ– bağıntısı sağlanır: Sıvının V2 Ol hızı kesitle ters orantılıdır. Basınç­larsa şu bağıntıyla belirlenir: Eı₊y₁i_=Ei+y2!. pg 2g pg 2g Dolayısıyla, en küçük kesite en yük­sek hız ve en düşük basınç denk düşer. Bu sonuçla, su emmeci ya da su trompuna (Bkz. çerçeve) ve türbin yayıcıları’na uygulanırlar. Borulardaki akışa, sıvının ağdalılığının yol açtığı bir yük yitimi eşlik eder. IX   = —+^-+Z miktarına akış yükü pg 2g     ^v  denir; belli bir uzunlukta ho­mojen olan bu büyüklük boru boyunca azalır. Boru silindir biçimli ve yatay (Çiz. 3) olduğunda V ile Z sabittir ve L uzunluğu için yük yitimi AX = Ei-Z-fi olur.

P9 Dolayısıyla yük yitimi bir basınç azalmasıyla açıklanır. Boyutsuz bir sayı olan j = A* oranına doğrusal yük yitimi denir. Bu yitim, yalnızca, özgül kütlesi ve ağdalılık katsayısı aracılı­ğıyla sıvıya değil, bunun hızına ve borunun boyutlarına da bağlıdır. Düşük hızda ya da çapı küçük olan borulardaki akış laminerdir: Çeşitli sıvı tabakaları karışmadan birbirle­rinin üstünde kayarlar. Boru ekseninde sıfır olan ağdalılık kuvvetleri, eksenden uzaklaştıkça artarlar. Bunun sonucu olarak da, parabol biçimli bir hız profili oluşur (Çiz. 4); boruyla temas eden tanecik­lerin (sınır tabaka) hızı sıfırdır. Poiseuille bağıntısı borunun hacimsel debisinin hesaplanmasını sağlar: Q = ^ D⁴; burada n, dinamik ağdalılık katsayısı; D borunun çapı; ise, birim uzunluktaki basınç değişimidir.

Sanayi kanallarında olduğu gibi yük­sek hızlar için düzen burgaçlıdır (türbülanslıdır): Sıvı, burgaçlı kaynaş­malarla donanmıştır.

Yük yitimleri ve debiler deneysel for­müllerle hesaplanırlar; nitekim, akış hızı çok sayıda etkene bağımlı oldu­ğundan, herhangi bir genel formül oluşturulamaz. Bu iki akış hızı ara­sındaki ayrım Reynolds sayısı aracı­lığıyla yapılır. Belirli bir kritik değer (yaklaşık 2 000) altındaki R Reynolds sayıları için hız laminerdir; bu değe­rin üstündeki sayılar burgaçlı hıza denk düşerler.

Kanallardaki Akış

Kanallardaki akış, borulardaki akış­la aynı olan bir davranış biçimi göste­rir. 1000’den küçük R için her zaman laminer, 2 500’den büyük R içinse her zaman burgaçlıdır; bu, çoğunlukla açık kanallar için söz konusu olur. Akışı düzenleyen büyüklükler eğim, debi ve derinliktir. Kesitin biçimi ve çeperlerin yapısı, uygulamalar göz önünde bulundurularak önerilirler. Yarım daire ve yarım kare, biçimli kesitlerin kuramsal olarak en iyileri­dir ama, gerçekleştirme açısından pahalıya mal olurlar. Kanal duvarlı olduğunda dikdörtgen, yer altında olduğundaysa yamuksu kesitler seçi­lir: Yer altındakilerde, kesit, merkezi suyun serbest yüzeyinde olan bir yarım daire biçiminde alınır. Çeper­lerin hızla yıpranmasını önlemek için hızın belli bir ortalama değeri aşma­ması sağlanır; bu değer çamurlu top­raklardaki 0,12 m/sn değeriyle kaya­lardaki 3,50 m/sn değeri arasında değişir. İki çeşit akış rejimi (düzeni) vardır: Ortalama hızın belli bir V_c kritik hız altında (serbest yüzdeki bir çalkantı­nın geliş yönüne doğru yayılabilmesiyle nitelenir) bulunduğu akarsu rejimi ve ortalama hızın V_c kritik hız­dan yüksek olduğu sel rejimi. Bu durumda hiçbir çalkantı, akıntının ters yönünde yayılamaz.

Öbür Uygulamalar

Hidrodinamik araştırmaları, çeşitli doğrultularda geliştirilmektedir: Türbinler, pompalar, baraj savak­ları, gemi karinaları, denizaltı profil­leri ve yağlamayla ilgili incelemeler. Deneysel inceleme, kuramsal incele­meye eşlik eder, hatta kuramsal ince­lemeden önce gelir. Maketler üstünde gerçekleştirilen deneysel incelemeler, benzeşim yasalarının uygulanmasını gerektirir. Sıvı damarın ayrılma etki­leri ve türbinlerin çark kanatları düzeyindeki çukurlukları, baraj savaklarında burgaçların oluşumu ve bunların aşındırıcı etkileri ancak deneysel incelemelerle belirlene­bilir.

Su Emmeci

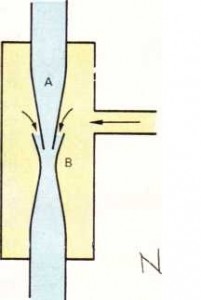
Su emmeci (su trompu), bir kapta kısmi vakum oluşturulmasını sağlar. Kullanımı çok basittir (bir su muslu­ğuna takmak yeterlidir), ancak, suyu doyuran buharın basıncıyla sınırlıdır (olağan sıcakhkta yaklaşık 20 torr ya da 2 700 pascal). Koni biçimli A lüle­sinden çıkan sıvı damar, ağdalılık nedeniyle kendisini çevreleyen hava­yı sürükler; ters koni biçimindeki B lülesine girdiğinde damar çevresinde bir kılıf oluşur. Bu kılıf yeterli bir inceliğe ulaştığında damarın suyu içinde emülsiyon oluşturur ve su, mekanik olarak oluşan kabarcıkları sürükler.